transformer位置编码研究

transformer位置编码初探

笔者在研究NLP和LLM时发现，位置编码至关重要。从Transformer开山之作（Attention is all you need）中的绝对位置编码，到llama中的旋转位置编码，有各种各样。博客中笔者列举了一些常见的位置编码，并分析其中的原理。

Transformer架构

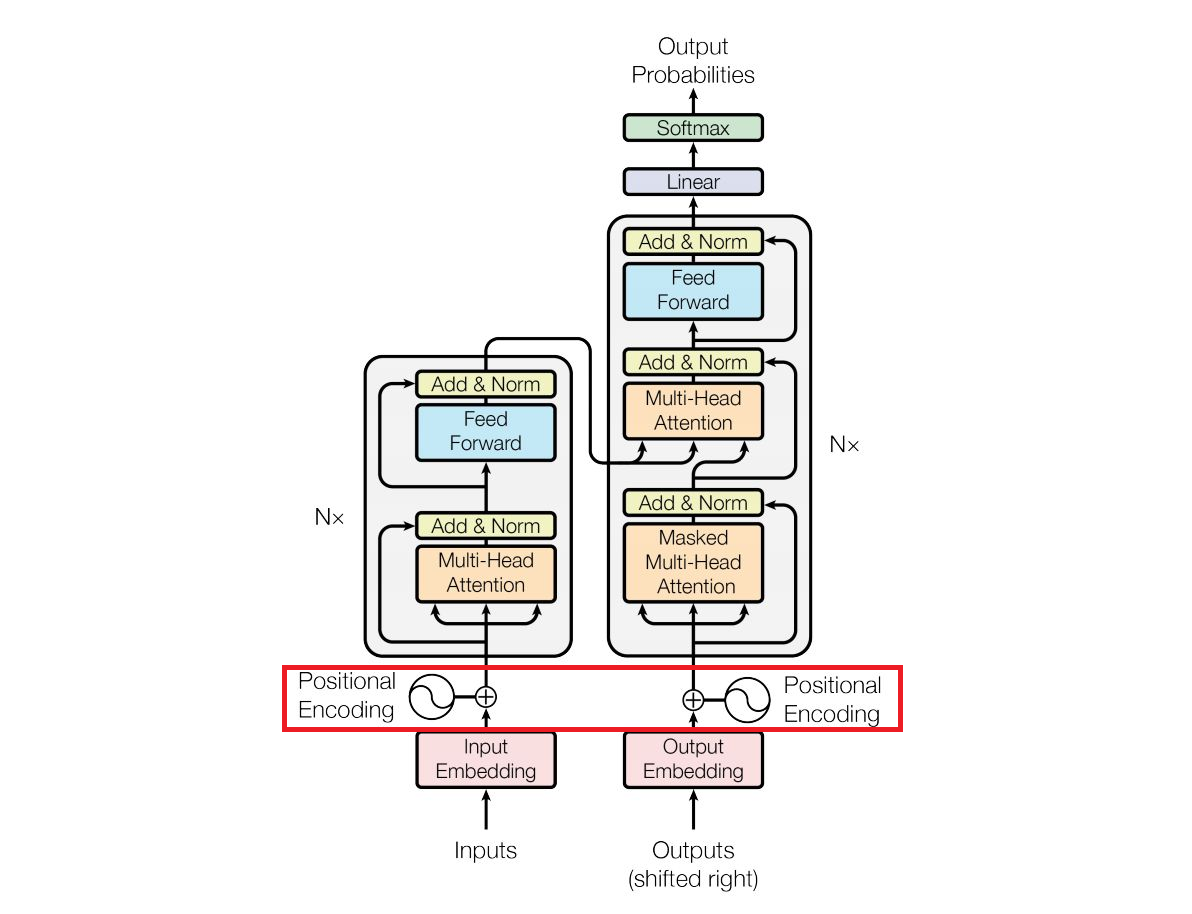
为什么需要位置编码

Attention没有关注位置信息。在NLP中，很显然同一个词在不同的位置有截然不同的意义。如”他对我说“和”我对他说“。因此引入位置编码（Positional Embedding）记录每个token的位置信息。将PE和原单词的嵌入向量相加，输入Transformer模型加以训练。

此外，位置编码和大模型外推性息息相关。

大模型的外推性指的是训练与预测时长度不一致。一般俩说，预测时上下文长度远大于训练时，容易出现泛化能力下降。选取合适的位置编码能够提升外推能力。

原始论文中Sinusoidal编码

$$ PE_{pos,2i} = sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) $$

$$ PE_{pos,2i+1} = cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) $$

即 $$ \left[ \begin{matrix} PE_{pos} = [sin(\omega_1\cdot{pos})] \\ PE_{pos} = [cos(\omega_1\cdot{pos})] \\ PE_{pos} = [sin(\omega_2\cdot{pos})] \\ PE_{pos} = [cos(\omega_2\cdot{pos})] \\ \ldots \\ PE_{pos} = [sin(\omega_{\frac{d}{2}}\cdot{pos})] \\ PE_{pos} = [cos(\omega_{\frac{d}{2}}\cdot{pos})] \end{matrix} \right] $$

采用sin和cos奇偶交替，具有平滑性、不会重复。

其中PE代表位置编码，pos代表每个单词的位置，0,1,2,3……。d_{model}代表嵌入维度。

由于 $$ 0 \le \frac{2i}{d_{model}} \le 1, \\ 有 1 \le 10000^{\frac{2i}{d_{model}}} \le 10000 $$ 另外可观察到，对于同一个向量分量，PE随着pos呈现正弦或余弦波动。

周期为： $$ T = 2 \pi \cdot 10000^{\frac{2i}{d_{model}}} $$ 随着i的增大而增大。

旋转位置编码原理

1
2
3
4
5
6

def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    t = torch.arange(end, device=freqs.device, dtype=torch.float32)
    freqs = torch.outer(t, freqs)
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis

torch.polar： 将极坐标 $$ (\rho, \theta) $$ 转化为复数坐标 $$ (\rho cos\theta, \rho sin\theta \cdot i) $$ torch.arange：pytorch中生成有序列表。

torch.ones_like：生成全为1的形状相同tensor。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

• view_as_comlex

  作用：将一个实数张量视为一个复数张量。

  • 输入要求：输入张量的最后一个维度的大小必须为 2，表示复数的实部和虚部。例如，一个形状为 [batch_size, seq_len, 2] 的张量，其中最后一个维度表示实部和虚部。
  • 转换结果：该函数将输入的实数张量转换为复数张量。最后一个维度中的第一个数被视为复数的实部，第二个数被视为虚部。

• view_as_real

  作用：将一个复数张量转换为实数张量。

  • 输入要求：输入必须是一个复数张量。

• 转换结果：该函数会将复数张量转换为一个实数张量，其中最后一个维度表示复数的实部和虚部。结果张量的形状会比原来的复数张量多一个维度（最后一维的大小为 2）。

代码巧妙地先把向量中的元素两两转为复数，与freqs_cis相乘后，再转回实数表达形式并合并。

旋转位置编码推导

b站上有大佬对旋转位置编码进行详细的推导。简而言之，核心在于巧用欧拉公式。 $$ e^{i\theta} = cos\theta+isin\theta $$

用到的主要是欧拉公式和高中三角函数知识，在草稿纸上可以推演一番。